https://en.wikipedia.org/wiki/Multi-armed_bandit
In probability theory, the multi-armed bandit problem (sometimes called the K- or N-armed bandit problem) is a problem in which a gambler at a row of slot machines (sometimes known as “one-armed bandits”) has to decide which machines to play, how many times to play each machine and in which order to play them. When played, each machine provides a random reward from a distribution specific to that machine. The objective of the gambler is to maximize the sum of rewards earned through a sequence of lever pulls.
(Phys.org)—A combined team of researchers from France and Japan has created a decision-making device that is based on basic properties of quantum mechanics. In their paper published in Scientific Reports (and uploaded to the arXiv preprint server), the team describes the idea behind their device and how it works.
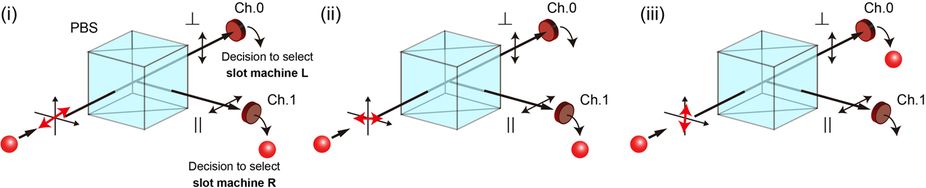
There is a classic decision-making problem that is known as the exploration-exploitation dilemma—it is typically described by suggesting a scenario where a gambler faced with a floor full of slot machines must decide which offers the best payout on a regular basis. In real life, the solution involves feeding all of the machines coins until a discernible pattern emerges. Computer algorithms have been developed to run essentially the same process. Now, however, that approach appears to be ready for an update, as the researchers with this new effort have come up with a way to run the same sort of algorithm without using any kind of computer. Instead, they use a laser, a photon detector and feedback device. The idea is based on the fact that quantum mechanics laws are probabilistic in nature.
The device is based on prior research that has shown that if photons are fired from a proton gun at a 45 degree angle, they will each have an equal chance of being vertically or horizontally polarized when they strike a detector—thus a stream will have equal numbers of both. But, if the filter on the gun is changed slightly, to say fire at 44 or 46 degree angles, that increase the odds of the associated polarization. The team used that fact by adding a feedback loop to the system—data sent back representing a “win” on a slot machine caused the filter to move in one direction, while a loss moved it in the other. Over time, the preponderance of wins (indicating a learning process) from one virtual machine would drive the device towards indicating it was the winning choice.