Basically all this says is that a basic quantum computer made of a simulation of an infinite quantum computer. So essentially infinite quantum computers could make the internet much more instant.
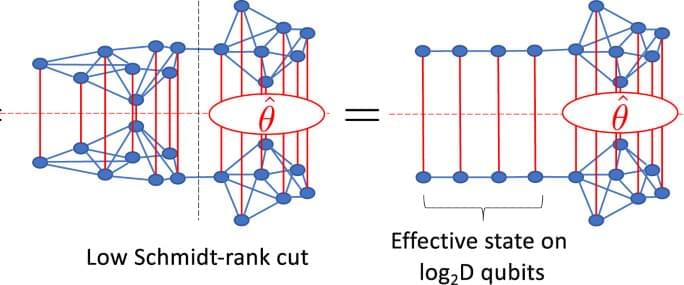
To parallelise our simulation on a small NISQ machine, we first identify partitions of the system where the effect of one partition upon the other can be summarised by a small amount of information. This is achieved by making Schmidt decompositions across the cut: \(\left|\psi \right\rangle =\mathopsum
olimits_alpha = 1Dlambda ^alpha \left|phi _L^alpha \right\rangle \left|phi _R^alpha \right\rangle,\) where \(\left|phi _L^alpha \right\rangle\) are an orthonormal set of states to the left of the cut and \(\left|phi _R^alpha \right\rangle\) the same on the right. The λα are known as the Schmidt coefficients and D the Schmidt rank or bond order. Retaining λα only above some threshold value provides a way to compress representations of a quantum state; the MPS construction can be obtained by applying this procedure sequentially along a spin chain4.
If an observation is made on the right-hand-side of such a cut, the effect of the quantum state on the left upon the observation can be summarised by just D variables corresponding to the Schmidt coefficients. This same effect can be achieved by an effective state on a spin chain of length \(log\,_2D\) —see Fig. 1 —which can be parametrised on the quantum circuit by an SU (D2) unitary VL. This encodes both the Schmidt coefficients λα and the orthonormal states \(\left|phi _L^alpha \right\rangle\). The latter does not contribute to observables on the right and so in principle, VL can be parametrised by just D variational parameters. The precise numerical values must be determined by solving a quantum mechanical problem on the left of the system. Similarly, for observations made to the left of the cut, the effect of the right-hand side can be summarised by a unitary VR.