Lifeboat Foundation

face_with_colon_three year 2017.

First observed in liquid helium below the lambda point, superfluidity manifests itself in a number of fascinating ways. In the superfluid phase, helium can creep up along the walls of a container, boil without bubbles, or even flow without friction around obstacles. As early as 1938, Fritz London suggested a link between superfluidity and Bose–Einstein condensation (BEC)³. Indeed, superfluidity is now known to be related to the finite amount of energy needed to create collective excitations in the quantum liquid^4,5,6,7, and the link proposed by London was further evidenced by the observation of superfluidity in ultracold atomic BECs^1,8. A quantitative description is given by the Gross–Pitaevskii (GP) equation^9,10 (see Methods) and the perturbation theory for elementary excitations developed by Bogoliubov¹¹. First derived for atomic condensates, this theory has since been successfully applied to a variety of systems, and the mathematical framework of the GP equation naturally leads to important analogies between BEC and nonlinear optics^12,13,14. Recently, it has been extended to include condensates out of thermal equilibrium, like those composed of interacting photons or bosonic quasiparticles such as microcavity exciton-polaritons and magnons^14,15. In particular, for exciton-polaritons, the observation of many-body effects related to condensation and superfluidity such as the excitation of quantized vortices, the formation of metastable currents and the suppression of scattering from potential barriers^{2,16,17,18,19,20} have shown the rich phenomenology that exists within non-equilibrium condensates. Polaritons are confined to two dimensions and the reduced dimensionality introduces an additional element of interest for the topological ordering mechanism leading to condensation, as recently evidenced in ref. 21. However, until now, such phenomena have mainly been observed in microcavities embedding quantum wells of III–V or II–VI semiconductors. As a result, experiments must be performed at low temperatures (below ∼ 20 K), beyond which excitons autoionize. This is a consequence of the low binding energy typical of Wannier–Mott excitons. Frenkel excitons, which are characteristic of organic semiconductors, possess large binding energies that readily allow for strong light–matter coupling and the formation of polaritons at room temperature. Remarkably, in spite of weaker interactions as compared to inorganic polaritons²², condensation and the spontaneous formation of vortices have also been observed in organic microcavities^23,24,25. However, the small polariton–polariton interaction constants, structural inhomogeneity and short lifetimes in these structures have until now prevented the observation of behaviour directly related to the quantum fluid dynamics (such as superfluidity). In this work, we show that superfluidity can indeed be achieved at room temperature and this is, in part, a result of the much larger polariton densities attainable in organic microcavities, which compensate for their weaker nonlinearities.

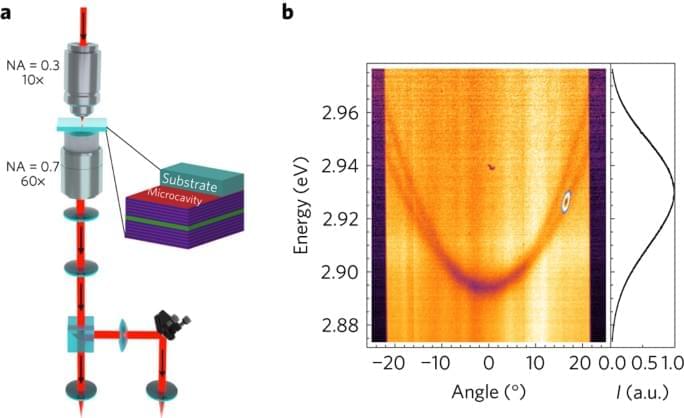
Our sample consists of an optical microcavity composed of two dielectric mirrors surrounding a thin film of 2,7-Bis[9,9-di(4-methylphenyl)-fluoren-2-yl]-9,9-di(4-methylphenyl)fluorene (TDAF) organic molecules. Light–matter interaction in this system is so strong that it leads to the formation of hybrid light–matter modes (polaritons), with a Rabi energy 2 Ω_R ∼ 0.6 eV. A similar structure has been used previously to demonstrate polariton condensation under high-energy non-resonant excitation²⁴. Upon resonant excitation, it allows for the injection and flow of polaritons with a well-defined density, polarization and group velocity.

The experimental configuration is shown in Fig. 1a. The sample is positioned between two microscope objectives to allow for measurements in a transmission geometry while maintaining high spatial resolution. A polariton wavepacket with a chosen wavevector is created by exciting the sample with a linearly polarized 35 fs laser pulse resonant with the lower polariton branch (see Methods). By detecting the reflected or transmitted light using a spectrometer and a charge-coupled device (CCD) camera, energy-resolved space and momentum maps can be acquired. An example of the experimental polariton dispersion under white light illumination is shown in Fig. 1b. The parabolic TE-and TM-polarized lower polariton branches appear as dips in the reflectance spectra. The figure also shows an example of how the laser energy, momentum and polarization can be precisely tuned to excite, in this case, the TE lower polariton branch at a given angle.