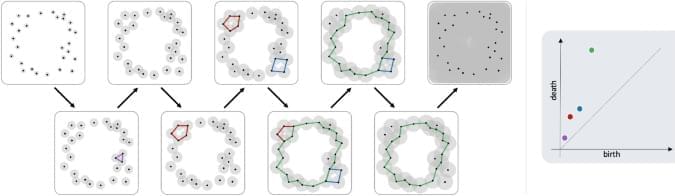
One of the key challenges in TDA is to distinguish between “signal”—meaningful structures underlying the data, and “noise”—features that arise from the local randomness and inaccuracies within the data15,16,17. The most prominent solution developed in TDA to address this issue is persistent homology. Briefly, it identifies structures such as holes and cavities (“air pockets”) formed by the data, and records the scales at which they are created and terminated (birth and death, respectively). The common practice in TDA has been to use this birth-death information to assess the statistical significance of topological features18,19,20,21. However, research so far has yet to provide an approach which is generic, robust, and theoretically justified. A parallel line of research has been the theoretical probabilistic analysis of persistent homology generated by random data, as means to establish a null-distribution. While this direction has been fruitful22,23,24,25, its use in practice has been limited. The main gap between theory and practice is that these studies indicate that the distribution of noise in persistent homology: (a) does not have a simple closed-form description, and (b) strongly depends on the model generating the point-cloud.
Our main goal in this paper is to refute the last premise, and to make the case that the distribution of noise in persistent homology of random point-clouds is in fact universal. Specifically, we claim that the limiting distribution of persistence values (measured using the death/birth ratio) is independent of the model generating the point-cloud. This result is loosely analogous to the central limit theorem, where sums of many different types of random variables always converge to the normal distribution. The emergence of such universal ity for persistence diagrams is highly surprising.
We support our universal ity statements by an extensive body of experiments, including point-clouds generated by different geometries, topologies, and probability distributions. These include simulated data as well as data from real-world applications (image processing, signal processing, and natural language processing). Our main goal here is to introduce the unexpected behavior of statistical universal ity in persistence diagrams, in order to initiate a shift of paradigm in stochastic topology that will lead to the development of a new theory. Developing this new theory, and proving the conjectures made here, is anticipated to be an exciting yet a challenging long journey, and is outside the scope of this paper. Based on our universal ity conjectures, we develop a powerful hypothesis testing framework for persistence diagrams, allowing us to compute numerical significance measures for individual features using very few assumptions on the underlying model.