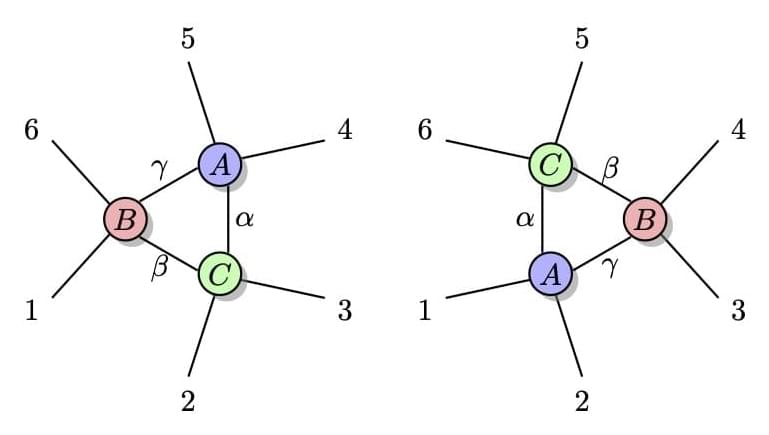
Balázs Pozsgay and Ian M. Wanless, Quantum 8, 1339 (2024). Absolutely maximally entangled (AME) states of $k$ qudits (also known as perfect tensors) are quantum states that have maximal entanglement for all possible bipartitions of the sites/parties. We consider the problem of whether such states can be decomposed into a tensor network with a small number of tensors, such that all physical and all auxiliary spaces have the same dimension $D$. We find that certain AME states with $k=6$ can be decomposed into a network with only three 4-leg tensors; we provide concrete solutions for local dimension $D=5$ and higher. Our result implies that certain AME states with six parties can be created with only three two-site unitaries from a product state of three Bell pairs, or equivalently, with six two-site unitaries acting on a product state on six qudits. We also consider the problem for $k=8$, where we find similar tensor network decompositions with six 4-leg tensors.
Comments are closed.