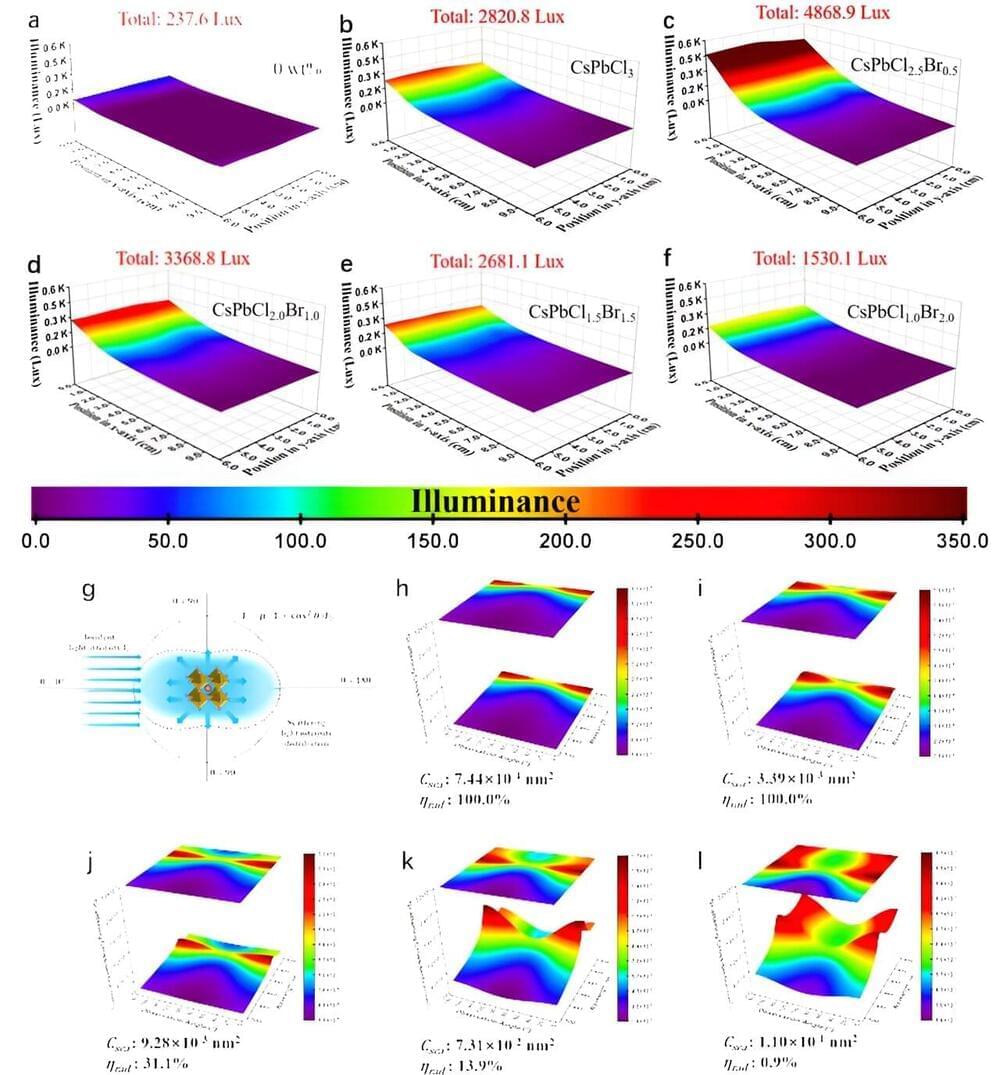
The fact that nanoparticle and polymer hybrid materials can often combine the advantages of each has been demonstrated in several fields. Embedding PNCs into polymer is an effective strategy to enhance the PNCs stability and polymer can endow the PNCs with other positive effects based on different structure and functional groups.
The uniform distribution of PNCs in polymer matrix is critical to the properties of the nanocomposites and the aggregation of PNCs induced by high surface energy has a severe influence on the performance of related applications. As such, the loading fraction is limited owing to the phase separation between PNCs and polymer.
Chemical interaction between PNCs and polymer is necessary to suppress the phase separation. Meanwhile, most of the fabrication methods of PNCs/polymer nanocomposites are spin coating, swelling-shrinking and electrospinning based on the in-situ synthesis of PNCs in polymer matrix and physical mixing, but extremely few works can achieve the fabrication of PNCs/polymer nanocomposites by bulk polymerization.