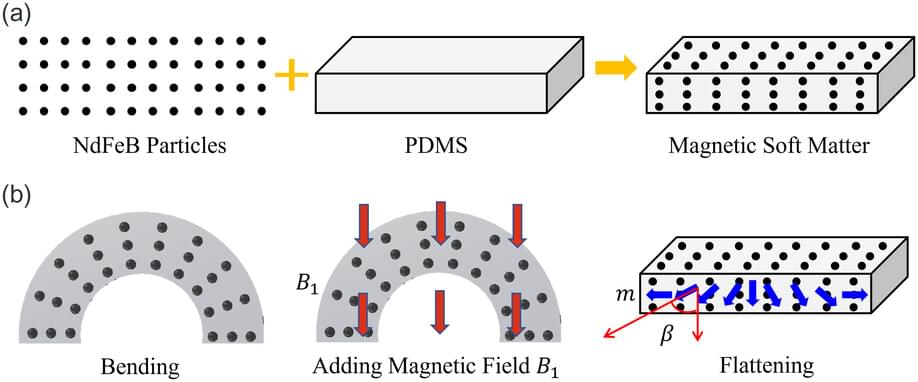
Soft materials and magnetic fields enable a new generation of dexterous, fast-moving microrobotic joints for complex object manipulation tasks.

New materials engineered to be both stiff and heat-insulating could revolutionize thermal insulation applications in electronics.
Scientists have successfully engineered materials that are both rigid and effective at insulating against heat. This extremely rare combination of attributes offers significant potential for various applications, including the creation of new thermal insulation coatings for electronic devices.
“Materials that have a high elastic modulus tend to also be highly thermally conductive, and vice versa,” says Jun Liu, co-corresponding author of a paper on the work and an associate professor of mechanical and aerospace engineering at North Carolina State University. “In other words, if a material is stiff, it does a good job of conducting heat. And if a material is not stiff, then it is usually good at insulating against heat.
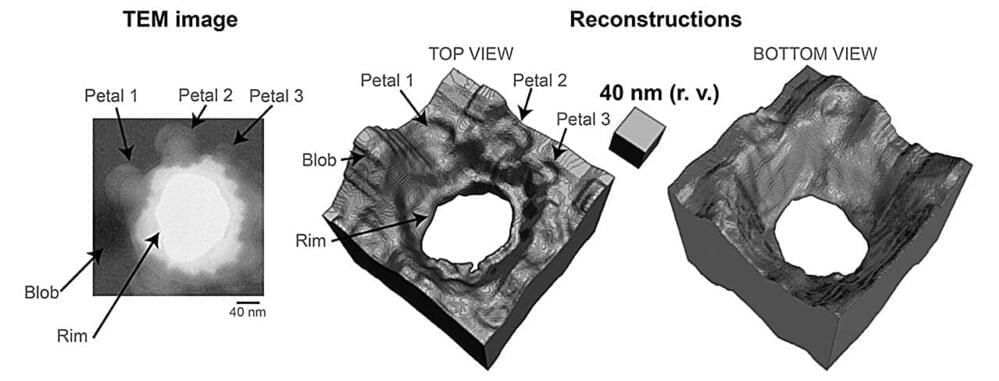
Dr. Deepan Balakrishnan, the first author, said, “Our work shows the theoretical framework for single-shot 3D imaging with TEMs. We are developing a generalized method using physics-based machine learning models that learn material priors and provide 3D relief for any 2D projection.”
The team also envisions further generalizing the formulation of pop-out metrology beyond TEMs to any coherent imaging system for optically thick samples (i.e., X-rays, electrons, visible light photons, etc.).
Prof Loh added, “Like human vision, inferring 3D information from a 2D image requires context. Pop-out is similar, but the context comes from the material we focus on and our understanding of how photons and electrons interact with them.”

Water is usually something you’d want to keep away from electronic circuits, but engineers in Germany have now developed a new concept for water-based switches that are much faster than current semiconductor materials.
Transistors are a fundamental component of electronic systems, and in a basic sense they process data by switching between conductive and non-conductive states – zeroes and ones – as the semiconductor materials in them encounter electrical currents. The speed of this switching (along with the number of transistors in a chip) is a primary factor in how fast a computer system can be.
Now, researchers at Ruhr University Bochum have developed a new type of circuit that can switch much faster than existing semiconductor materials. The key ingredient is, surprisingly, water, with iodide ions dissolved into it to make it salty. A custom-made nozzle fans this water out into a flattened jet only a few microns thick.

Graphene has been called “the wonder material of the 21st century.” Since its discovery in 2004, the material—a single layer of carbon atoms—has been touted for its host of unique properties, which include ultra-high electrical conductivity and remarkable tensile strength. It has the potential to transform electronics, energy storage, sensors, biomedical devices, and more. But graphene has had a dirty little secret: it’s dirty.

In the last year, two independent groups have observed electrons behaving like quasiparticles with fractional amounts of charge, like –²⁄₃ and –³⁄₅, without the influence of a magnetic field.
In the 127 years since the electron was discovered, it has undergone more scrutiny than perhaps any other particle. As a result, its properties are not just well known, but rote, textbook material: Electrons have a smidgen of mass and negative electric charge. In a conductor, they swim relatively unimpeded as a current; in an insulator, they barely move.
Over time, caveats have cropped up. Under an intense magnetic field, for example, electrons can lose their individual identities and form “quasiparticles”: collective entities, like the shape formed by a school of fish. But even these collective states have been well cataloged.
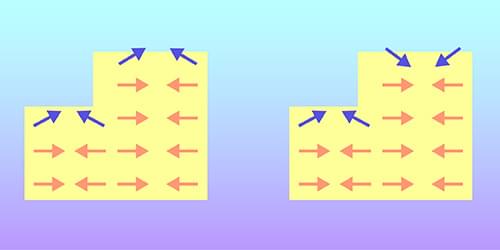
Group theory and first-principles calculations combine to predict which antiferromagnets have potentially useful net surface magnetization.
Antiferromagnetism was discovered in the 1930s by Louis Néel but had long been considered of scientific, not practical, interest. Antiferromagnets (AFM) are internally magnetic, but the magnetic moments of their atoms and molecules are antiparallel to each other, canceling out and resulting in no net magnetization. This cancellation renders bulk antiferromagnets effectively invisible to external magnetic fields, so that their magnetic properties are difficult to harness in applications. Recently, however, a new paradigm has appeared—antiferromagnetism-based spintronics—which seeks to apply antiferromagnets’ unique properties (such as fast spin dynamics, the absence of strong stray fields, and the stability of these materials) to the processing and storage of information [1].
Lithium-ion batteries have been at the forefront of energy storage technologies. However, the availability of lithium is limited. Consequently, the growing demand for energy-storage systems has led to the search for low-cost and more accessible materials for rechargeable batteries. Sodium-ion batteries (SIBs) are a promising candidate due to the virtually unlimited sodium (Na) resources in seawater and salt deposits.

One way to manage the unsustainable energy requirements of the computing sector is to fundamentally change the way we compute. Superconductors could let us do just that.
Superconductors offer the possibility of drastically lowering energy consumption because they do not dissipate energy when passing current. True, superconductors work only at cryogenic temperatures, requiring some cooling overhead. But in exchange, they offer virtually zero-resistance interconnects, digital logic built on ultrashort pulses that require minimal energy, and the capacity for incredible computing density due to easy 3D chip stacking.
Are the advantages enough to overcome the cost of cryogenic cooling? Our work suggests they most certainly are. As the scale of computing resources gets larger, the marginal cost of the cooling overhead gets smaller. Our research shows that starting at around 10 16 floating-point operations per second (tens of petaflops) the superconducting computer handily becomes more power efficient than its classical cousin. This is exactly the scale of typical high-performance computers today, so the time for a superconducting supercomputer is now.