A series of new papers describes how to fully characterize key dynamical systems with relatively little data.


The company now plans to power its quantum computers with a minimum of 127 qubits.
IBM’s Eagle quantum computer has outperformed a conventional supercomputer when solving complex mathematical calculations. This is also the first demonstration of a quantum computer providing accurate results at a scale of 100+ qubits, a company press release said.
Qubits, short for quantum bits, are analogs of a bit in quantum computing. Both are the primary or smallest units of information. However, unlike bits that can exist in two states, 0 or 1, a qubit can represent either of the states or in a superposition where it exists in any proportion of the two states.
Fibonacci numbers are seen in the natural structures of various plants, such as the florets in sunflower heads, areoles on cacti stems, and scales in pine cones. [HackerBox] has developed a Fibonacci Spiral LED Badge to bring this natural phenomenon to your electronics.
To position each of the 64 addressable LEDs within the PCB layout, [HackerBox] computed the polar (r,θ) coordinates in a spreadsheet according to the Vogel model and then converted them to rectangular (x, y) coordinates. A little more math translates the points “off origin” into the center of the PCB space and scale them out to keep the first two 5 mm LEDs from overlapping. Finally, the LED coordinates were pasted into the KiCad PCB design file.
An RP2040 microcontroller controls the show, and a switch on the badge selects power between USB and three AA batteries and a DC/DC boost converter. The PCB also features two capacitive touch pads. [HackerBox] has published the KiCad files for the badge, and the CircuitPython firmware is shared with the project. If C/C++ is more your preference, the RP2040 MCU can also be programmed using the Arduino IDE.
Editor’s note: For a more mainstream assessment of this idea, see this article by Dr. Ethan Siegel.
Sir Roger Penrose, a mathematician and physicist from the University of Oxford who shared the Nobel Prize in physics in 2020, claims our universe has gone through multiple Big Bangs, with another one coming in our future.
Penrose received the Nobel for his working out mathematical methods that proved and expanded Albert Einstein’s general theory of relativity, and for his discoveries on black holes, which showed how objects that become too dense undergo gravitational collapse into singularities – points of infinite mass.

For example, scientists have recently emphasized that the physical organization of the Universe mirrors the structure of a brain. Theoretical physicist Sabine Hossenfelder — renowned for her skepticism — wrote a bold article for Time Magazine in August of 2022 titled “Maybe the Universe Thinks. Hear Me Out,” which describes the similarities. Like our nervous system, the Universe has a highly interconnected, hierarchical organization. The estimated 200 billion detectable galaxies aren’t distributed randomly, but lumped together by gravity into clusters that form even larger clusters, which are connected to one another by “galactic filaments,” or long thin threads of galaxies. When one zooms out to envision the cosmos as a whole, the “cosmic web” formed by these clusters and filaments looks strikingly similar to the “connectome,” a term that refers to the complete wiring diagram of the brain, which is formed by neurons and their synaptic connections. Neurons in the brain also form clusters, which are grouped into larger clusters, and are connected by filaments called axons, which transmit electrical signals across the cognitive system.
Hossenfelder explains that this resemblance between the cosmic web and the connectome is not superficial, citing a rigorous study by a physicist and a neuroscientist that analyzed the features common to both, and based on the shared mathematical properties, concluded that the two structures are “remarkably similar.” Due to these uncanny similarities, Hossenfelder speculates as to whether the Universe itself could be thinking.
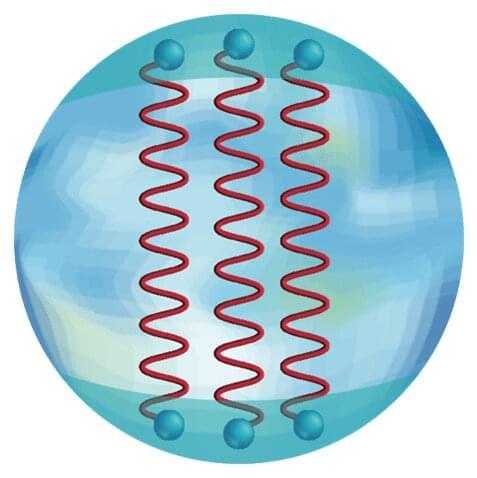
Understanding the behavior of nuclear matter—including the quarks and gluons that make up the protons and neutrons of atomic nuclei—is extremely complicated. This is particularly true in our world, which is three dimensional. Mathematical techniques from condensed matter physics that consider interactions in just one spatial dimension (plus time) greatly simplify the challenge.
Using this two-dimensional approach, scientists solved the complex equations that describe how low-energy excitations ripple through a system of dense nuclear matter. This work indicates that the center of neutron stars, where such dense nuclear matter exists in nature, may be described by an unexpected form.
Being able to understand the quark interactions in two dimensions opens a new window into understanding neutron stars, the densest form of matter in the universe. The approach could help advance the current “golden age” for studying these exotic stars. This surge in research success was triggered by recent discoveries of gravitational waves and electromagnetic emissions in the cosmos.
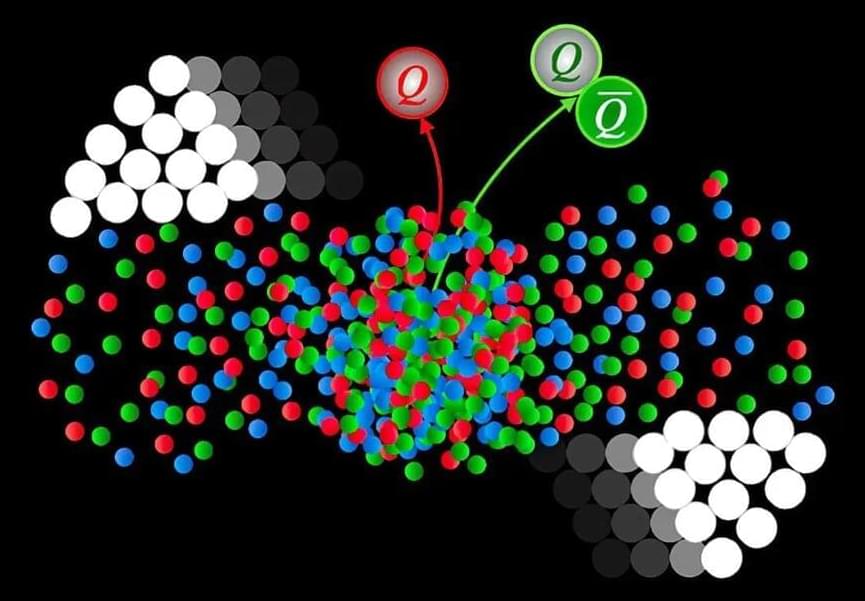
Scientists have taken a significant step forward in the study of the properties of quarks and gluons, the particles that make up atomic nuclei, by resolving a long-standing issue with a theoretical calculation method known as “axial gauge.” MIT
MIT is an acronym for the Massachusetts Institute of Technology. It is a prestigious private research university in Cambridge, Massachusetts that was founded in 1861. It is organized into five Schools: architecture and planning; engineering; humanities, arts, and social sciences; management; and science. MIT’s impact includes many scientific breakthroughs and technological advances. Their stated goal is to make a better world through education, research, and innovation.

David Smith, a retired print technician from the north of England, was pursuing his hobby of looking for interesting shapes when he stumbled onto one unlike any other in November.
When Smith shared his shape with the world in March, excited fans printed it onto T-shirts, sewed it into quilts, crafted cookie cutters or used it to replace the hexagons on a soccer ball —some even made plans for tattoos.
The 13-sided polygon, which 64-year-old Smith called “the hat”, is the first single shape ever found that can completely cover an infinitely large flat surface without ever repeating the same pattern.
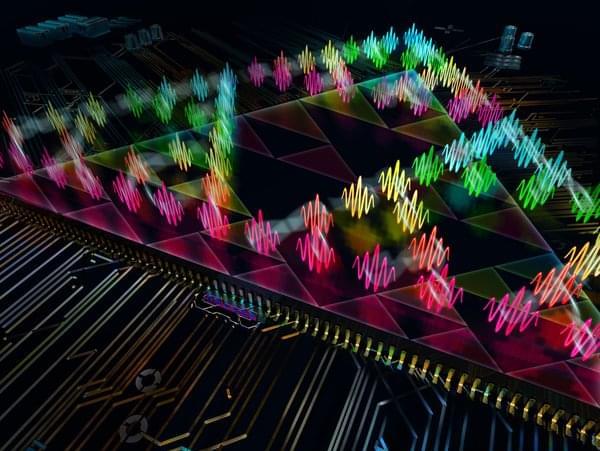
Basic, or “elementary,” cellular automata like The Game of Life appeal to researchers working in mathematics and computer science theory, but they can have practical applications too. Some of the elementary cellular automata can be used for random number generation, physics simulations, and cryptography. Others are computationally as powerful as conventional computing architectures—at least in principle. In a sense, these task-oriented cellular automata are akin to an ant colony in which the simple actions of individual ants combine to perform larger collective actions, such as digging tunnels, or collecting food and taking it back to the nest. More “advanced” cellular automata, which have more complicated rules (although still based on neighboring cells), can be used for practical computing tasks such as identifying objects in an image.
Marandi explains: “While we are fascinated by the type of complex behaviors that we can simulate with a relatively simple photonic hardware, we are really excited about the potential of more advanced photonic cellular automata for practical computing applications.”
Marandi says cellular automata are well suited to photonic computing for a couple of reasons. Since information processing is happening at an extremely local level (remember in cellular automata, cells interact only with their immediate neighbors), they eliminate the need for much of the hardware that makes photonic computing difficult: the various gates, switches, and devices that are otherwise required for moving and storing light-based information. And the high-bandwidth nature of photonic computing means cellular automata can run incredibly fast. In traditional computing, cellular automata might be designed in a computer language, which is built upon another layer of “machine” language below that, which itself sits atop the binary zeroes and ones that make up digital information.
