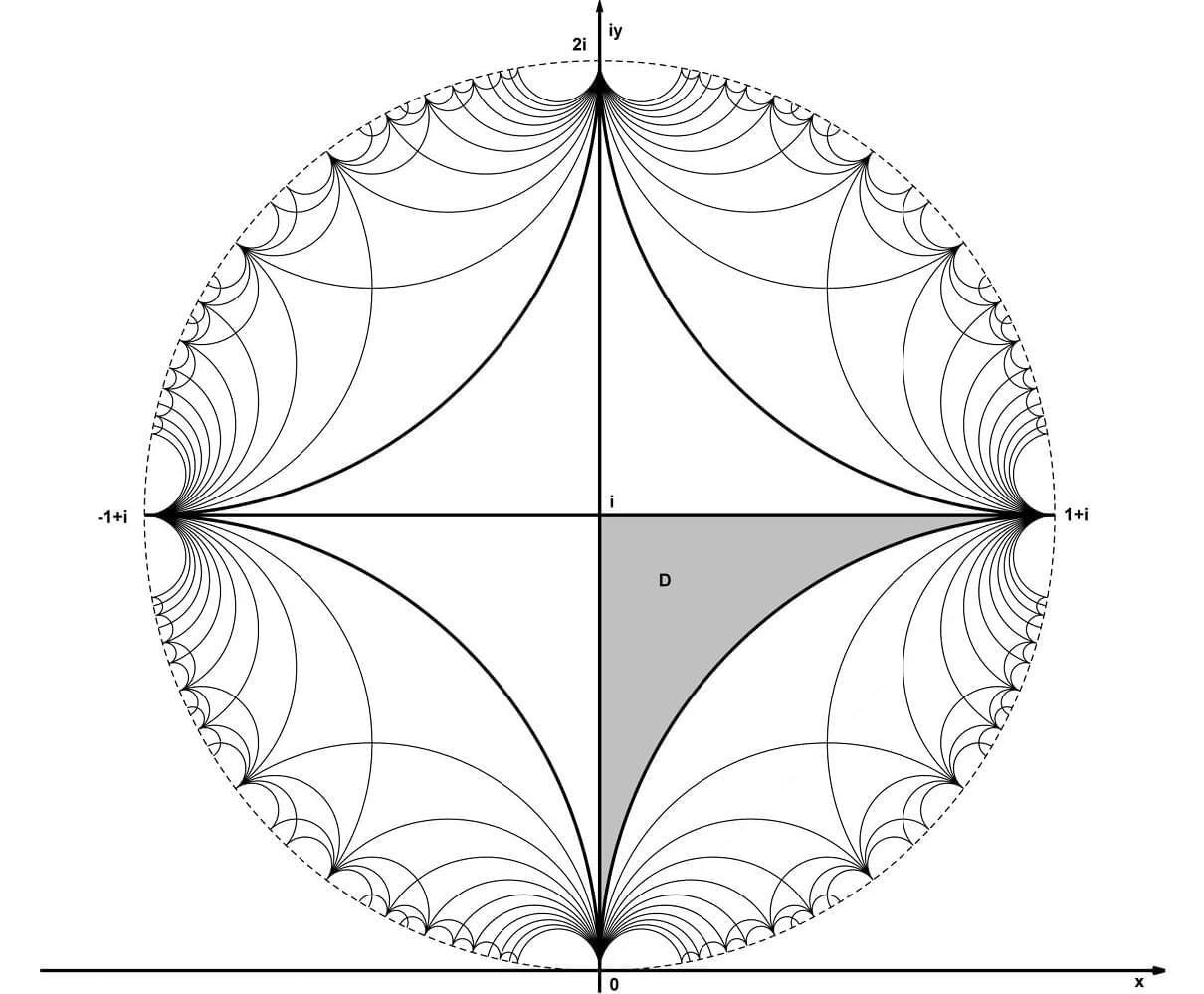
In a recent study, mathematicians from Freie Universität Berlin have demonstrated that planar tiling, or tessellation, is much more than a way to create a pretty pattern. Consisting of a surface covered by one or more geometric shapes with no gaps and no overlaps, tessellations can also be used as a precise tool for solving complex mathematical problems.
This is one of the key findings of the study, “Beauty in/of Mathematics: Tessellations and Their Formulas,” authored by Heinrich Begehr and Dajiang Wang and recently published in the scientific journal Applicable Analysis. The study combines results from the field of complex analysis, the theory of partial differential equations, and geometric function theory.
A central focus of the study is the “parqueting-reflection principle.” This refers to the use of repeated reflections of geometric shapes across their edges to tile a plane, resulting in highly symmetrical patterns. Aesthetic examples of planar tessellations can be seen in the work of M.C. Escher. Beyond its visual appeal, the principle has applications in mathematical analysis—for example, as a basis for solving classic boundary value problems such as the Dirichlet problem or the Neumann problem.