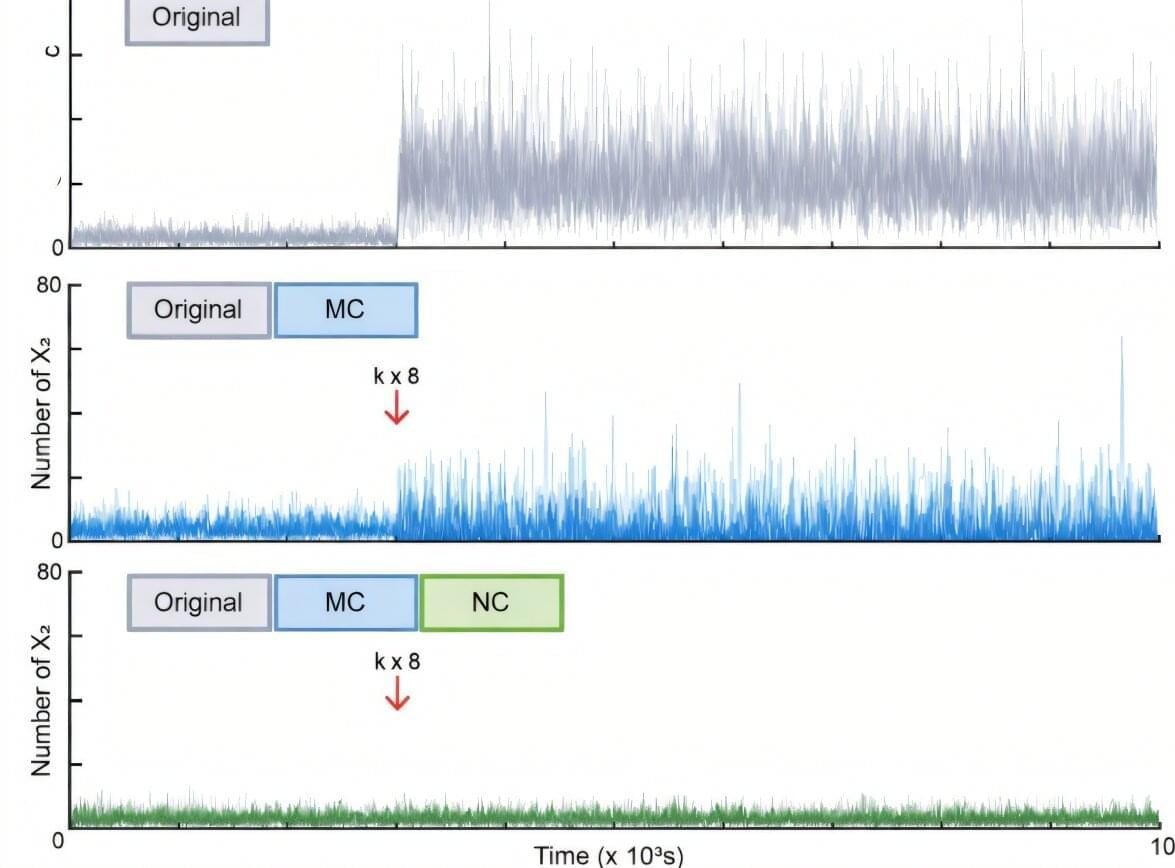
Why does cancer sometimes recur even after successful treatment, or why do some bacteria survive despite the use of powerful antibiotics? One of the key culprits identified is “biological noise”—random fluctuations occurring inside cells.
Even when cells share the same genes, the amount of protein varies in each, creating “outliers” that evade drug treatments and survive. Until now, scientists could only control the average values of cell populations; controlling the irregular variability of individual cells remained a long-standing challenge.
A joint research team—led by Professor Jae Kyoung Kim (Department of Mathematical Sciences, KAIST), Professor Jinsu Kim (Department of Mathematics, POSTECH), and Professor Byung-Kwan Cho (Graduate School of Engineering Biology, KAIST)—has theoretically established a “noise control principle.” Through mathematical modeling, they have found a way to eliminate biological noise and precisely govern cellular destiny.