Bose–Einstein Condensate (BEC) explained: Cool a dilute gas of atoms to billionths of a degree above absolute zero and they merge into one coherent matter wave—a Bose–Einstein condensate. This video covers laser cooling, magnetic/optical traps, evaporative cooling, the onset of quantum degeneracy, and why a BEC behaves like a superfluid. See signatures: interference fringes, quantized vortices, long coherence length, and frictionless flow. Applications include atom interferometers (precision gravity and rotation sensing), quantum simulation of complex materials, and space-based experiments (ISS Cold Atom Lab). We also touch on first BECs (1995, rubidium/sodium), critical temperature, and why bosons condense while fermions do not.
Category: particle physics – Page 10
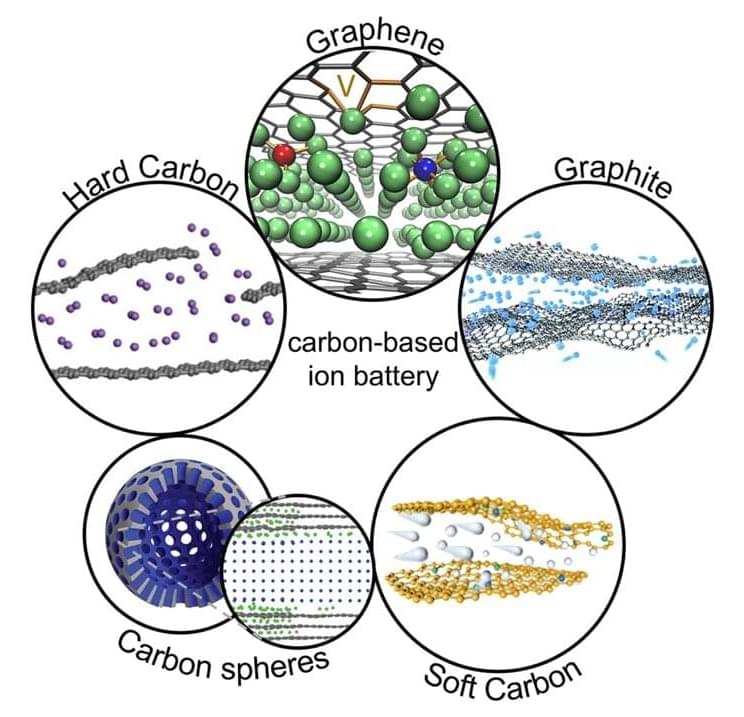
Safe and affordable fast-charging batteries: Multi-layered alkali metal structures open the door to energy of the future
Skoltech scientists conducted a study that advances research on future batteries. Their paper, published in Small, sheds light on recent advances in designing multilayered structures of alkali metals, such as lithium, sodium, and potassium, within carbon anode materials.
This technology has the potential to transform the energy storage market, enabling electric vehicles to charge in minutes and providing green energy with stable, safe, and affordable storage systems.
How multilayered structures improve batteries For years, ions were believed to form only single-atom layers in a battery’s carbon materials, such as graphite. In 2018, researchers used a high-precision electron microscope and discovered a new configuration with ultradense, multiatom layers of lithium forming between two sheets of graphene.


A Twist Between Hidden Dimensions May Explain Mass
The masses of fundamental particles such as the Z and W bosons could have arisen from the twisted geometry of hidden dimensions, a new theoretical paper has demonstrated.
The work has outlined a way to bypass the Higgs field as the source of particle masses, offering a new tool for understanding how the Higgs field itself might have emerged, as well as a possible means of addressing some of the persistent gaps in the Standard Model of particle physics.
“In our picture,” says theoretical physicist Richard Pinčák of the Slovak Academy of Sciences, “matter emerges from the resistance of geometry itself, not from an external field.”

Large Hadron Collider finally explains how fragile matter forms
In collisions at CERN’s Large Hadron Collider, hotter than the Sun’s core by a staggering margin, scientists have finally solved a long-standing mystery: how delicate particles like deuterons and their antimatter twins can exist at all. Instead of forming in the initial chaos, these fragile nuclei are born later, when the fireball cools, from the decay of ultra-short-lived, high-energy particles.
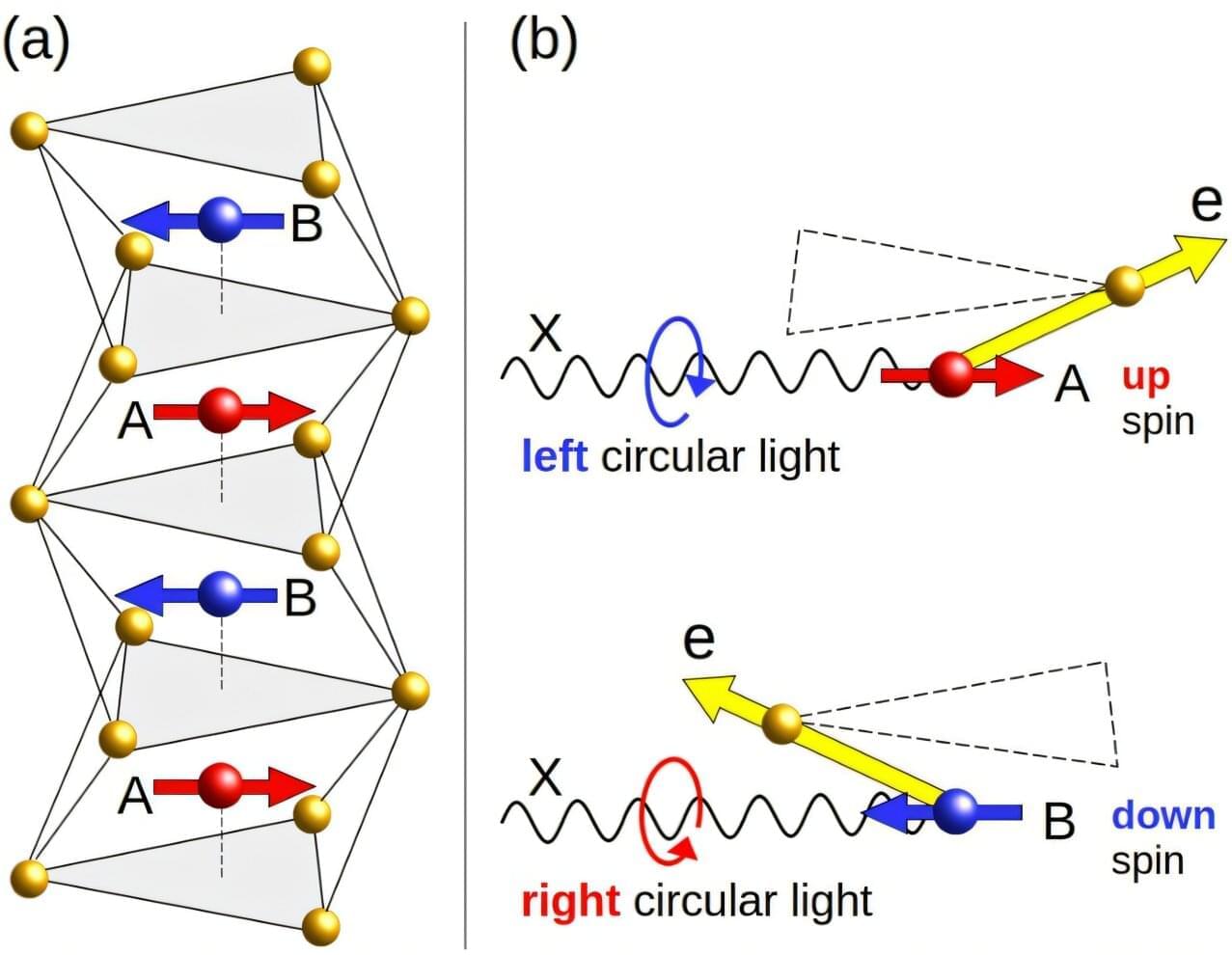
Detecting the hidden magnetism of altermagnets
Altermagnets are a newly recognized class of antiferromagnets whose magnetic structure behaves very differently from what is found in conventional systems. In conventional antiferromagnets, the sublattices are linked by simple inversion or translation, resulting in spin-degenerate electronic bands. In altermagnets, however, they are connected by unconventional symmetries such as rotations or screw axes. This shift in symmetry breaks the spin degeneracy, allowing for spin-polarized electron currents even in the absence of net magnetization.
This unique property makes altermagnets exciting candidates for spintronic technologies, a field of electronics that utilizes the intrinsic spin of the electrons, rather than just their charge, to store and process information. As spins can flip or switch direction extremely quickly, materials that allow spin-dependent currents could enable faster and more energy-efficient electronic devices.

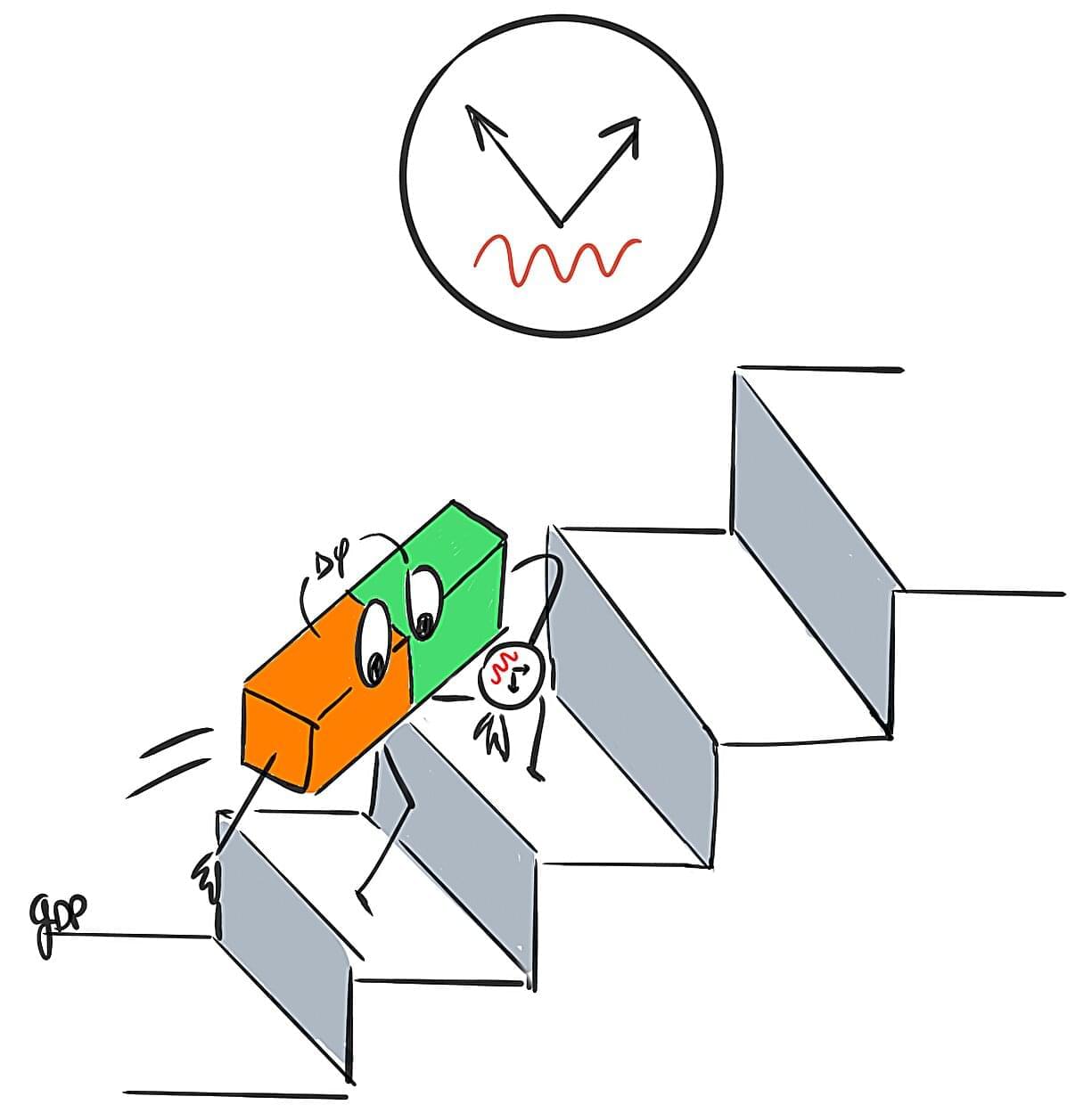
Ultracold atoms observed climbing a quantum staircase
For the first time, scientists have observed the iconic Shapiro steps, a staircase-like quantum effect, in ultracold atoms.
In a recent experiment, an alternating current was applied to a Josephson junction formed by atoms cooled to near absolute zero and separated by an extremely thin barrier of laser light. Remarkably, the atoms were able to cross this barrier collectively and without energy loss, behaving as if the barrier were transparent, thanks to quantum tunneling.
As the oscillating current flowed through the junction, the difference in chemical potential between the two sides did not change smoothly, but instead increased in discrete, evenly spaced steps, like climbing a quantum staircase. The height of each step is directly determined by the frequency of the applied current, and these step-like chemical potential differences are the atomic analog of Shapiro steps in conventional Josephson junctions.

