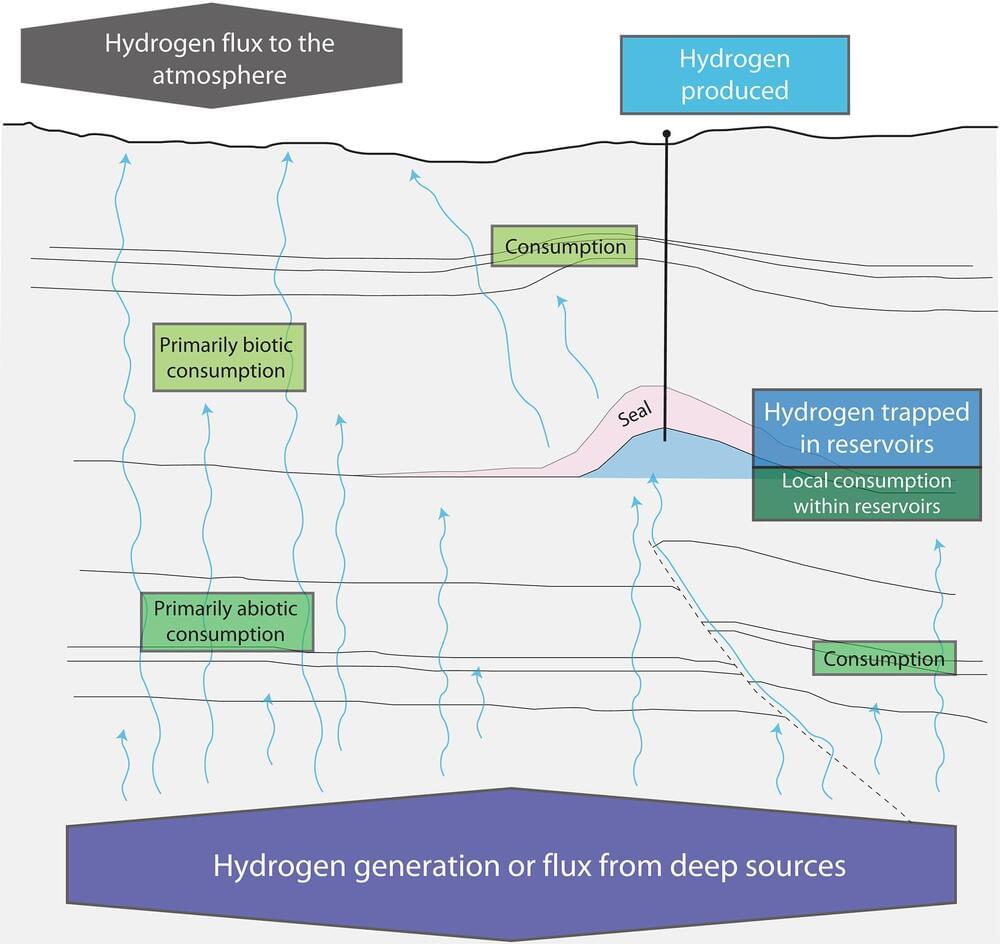
A pair of geologists with the U.S. Geological Survey, Denver, has created a model that shows Earth’s subsurface may hold up to 5.6 × 106 million metric tons of natural hydrogen. In their study, published in the journal Science Advances, Geoffrey Ellis and Sarah Gelman added factors to a geological model to produce estimates regarding the likely amount of hydrogen in parts of the Earth.
Prior research has shown that hydrogen can be produced artificially by applying electricity to water molecules to break them apart, leaving oxygen and hydrogen. Hydrogen is also produced naturally, via chemical reactions between rocks when they come into contact with one another. But until relatively recently, it was thought that very little hydrogen was made this way.
When geologists found huge natural reservoirs of hydrogen gas in Albania and West Africa, that thinking changed. Now, researchers believe that there are huge stores of hydrogen below our feet—the question remains, however, how to find it.