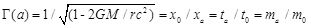If, we as a community, are intending to accelerate the development of interstellar travel we have to glower at the record and ask ourselves some tough questions. First, what is the current record of the primary players? Second, why is everyone afraid to try something outside the status quo theories?
At the present time the primary players are associated with the DARPA funded 100-Year Starship Study, as Icarus Interstellar who is cross linked with The Tau Zero Foundation and Centauri Dreams is a team member of the 100YSS. I was surprised to find Jean-Luc Cambier on Tau Zero.
Gary Church recently put the final nail in the Icarus Interstellar‘s dreams to build a rocket ship for interstellar travel. In his post on Lifeboat, Cosmic Ray Gorilla Gary Church says “it is likely such a shield will massive over a thousand tons”. Was he suggesting that the new cost of an interstellar rocket ship is not 3.4x World GDP but 34x or 340x World GDP? Oops!
Let us look at the record. Richard Obousy of Icarus Interstellar and Eric Davis of Institute for Advanced Studies claimed that it was possible, using string theories to travel at not just c, the velocity of light but at 1E32c, or c multiplied by a 1 followed by 32 zeros. However, Lorentz-FitzGerald transformations show that anything with mass cannot travel faster than the velocity of light. Note that Lorentz-FitzGerald is an empirical observation which was incorporated into Einstein’s Special Theory of Relativity.
It is quite clear that you can use string theories to say anything you want. I used the term ‘mathematical conjecture’.
In April 2008 the esteemed Michio Kaku said in his Space Show interview, that it would take several hundred years to do gravity modification. But Michio Kaku is a string theorist himself. And I might add down to Earth one at that, since his opinion contradicts Richard Obousy and Eric Davis.
Then there is George Hathaway also with the Tau Zero Foundation who could not reproduce Podkletnov’s experiments, even when he was in communication with Podkletnov.
And this is the one group our astronaut Mae Jemison, leader of the 100YSS effort, has teamed up with? My sincerest condolences to you Mae Jemison. Sincerest condolences.
For the answer to the second question, you have to look within yourselves.
—————————————————————————————————
Benjamin T Solomon is the author & principal investigator of the 12-year study into the theoretical & technological feasibility of gravitation modification, titled An Introduction to Gravity Modification, to achieve interstellar travel in our lifetimes. For more information visit iSETI LLC, Interstellar Space Exploration Technology Initiative.
Solomon is inviting all serious participants to his LinkedIn Group Interstellar Travel & Gravity Modification.