Recent research reveals that the immune system interacts with the body’s internal clock, influencing both fat storage and temperature regulation.
The discovery hints at why shift workers and others with irregular work, eating, or sleep patterns driven by the demands of modern life fall out of metabolic sync, and may hold potential for developing therapies to address obesity and prevent wasting.
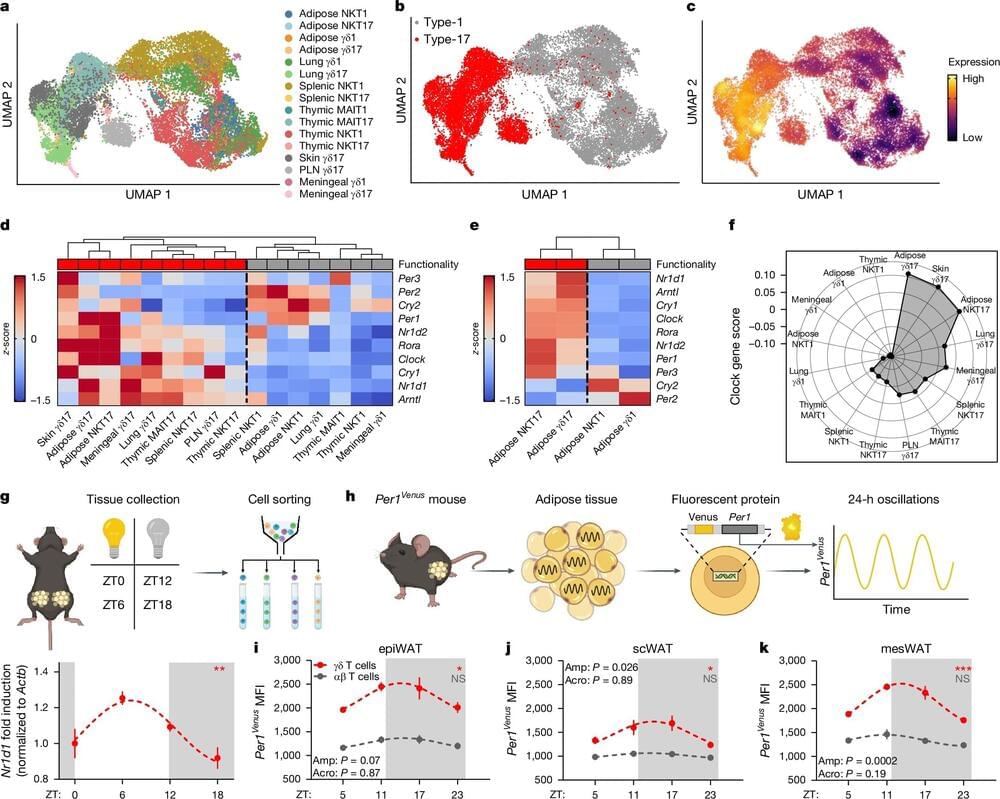
The key finding—that an immune molecule within adipose (fat) tissue, known as interleukin-17A (IL-17A), plays a regulatory role in fat storage—holds significant therapeutic potential for addressing obesity, preventing wasting, and mitigating other metabolic disorders. By targeting this molecule, drug developers may gain a valuable new pathway for creating treatments aimed at these conditions.