Edge AI isn’t a type of algorithm in and of itself, but it’s about where AI happens, regardless of the algorithm in question.



If new particles are out there, the Large Hadron Collider (LHC) is the ideal place to search for them. The theory of supersymmetry suggests that a whole new family of partner particles exists for each of the known fundamental particles. While this might seem extravagant, these partner particles could address various shortcomings in current scientific knowledge, such as the source of the mysterious dark matter in the universe, the “unnaturally” small mass of the Higgs boson, the anomalous way that the muon spins and even the relationship between the various forces of nature. But if these supersymmetric particles exist, where might they be hiding?
This is what physicists at the LHC have been trying to find out, and in a recent study of proton–proton collision data from Run 2 of the LHC (2015–2018), the ATLAS collaboration provides the most comprehensive overview yet of its searches for some of the most elusive types of supersymmetric particles—those that would only rarely be produced through the “weak” nuclear force or the electromagnetic force. The lightest of these weakly interacting supersymmetric particles could be the source of dark matter.
The increased collision energy and the higher collision rate provided by Run 2, as well as new search algorithms and machine-learning techniques, have allowed for deeper exploration into this difficult-to-reach territory of supersymmetry.

Researcher show that n-bit integers can be factorized by independently running a quantum circuit with orders of magnitude fewer qubits many times. It then use polynomial-time classical post-processing. The correctness of the algorithm relies on a number-theoretic heuristic assumption reminiscent of those used in subexponential classical factorization algorithms. It is currently not clear if the algorithm can lead to improved physical implementations in practice.
Shor’s celebrated algorithm allows to factorize n-bit integers using a quantum circuit of size O(n^2). For factoring to be feasible in practice, however, it is desirable to reduce this number further. Indeed, all else being equal, the fewer quantum gates there are in a circuit, the likelier it is that it can be implemented without noise and decoherence destroying the quantum effects.
The new algorithm can be thought of as a multidimensional analogue of Shor’s algorithm. At the core of the algorithm is a quantum procedure.

Each member works out within a designated station facing wall-to-wall LED screens. These tall screens mask sensors that track both the motions of the exerciser and the gym’s specially built equipment, including dumbbells, medicine balls, and skipping ropes, using a combination of algorithms and machine-learning models.
Once members arrive for a workout, they’re given the opportunity to pick their AI coach through the gym’s smartphone app. The choice depends on whether they feel more motivated by a male or female voice and a stricter, more cheerful, or laid-back demeanor, although they can switch their coach at any point. The trainers’ audio advice is delivered over headphones and accompanied by the member’s choice of music, such as rock or country.
Although each class at the Las Colinas studio is currently observed by a fitness professional, that supervisor doesn’t need to be a trainer, says Brandon Bean, cofounder of Lumin Fitness. “We liken it to being more like an airline attendant than an actual coach,” he says. “You want someone there if something goes wrong, but the AI trainer is the one giving form feedback, doing the motivation, and explaining how to do the movements.”
Large Language Models (LLMs) have gained a lot of attention for their human-imitating properties. These models are capable of answering questions, generating content, summarizing long textual paragraphs, and whatnot. Prompts are essential for improving the performance of LLMs like GPT-3.5 and GPT-4. The way that prompts are created can have a big impact on an LLM’s abilities in a variety of areas, including reasoning, multimodal processing, tool use, and more. These techniques, which researchers designed, have shown promise in tasks like model distillation and agent behavior simulation.
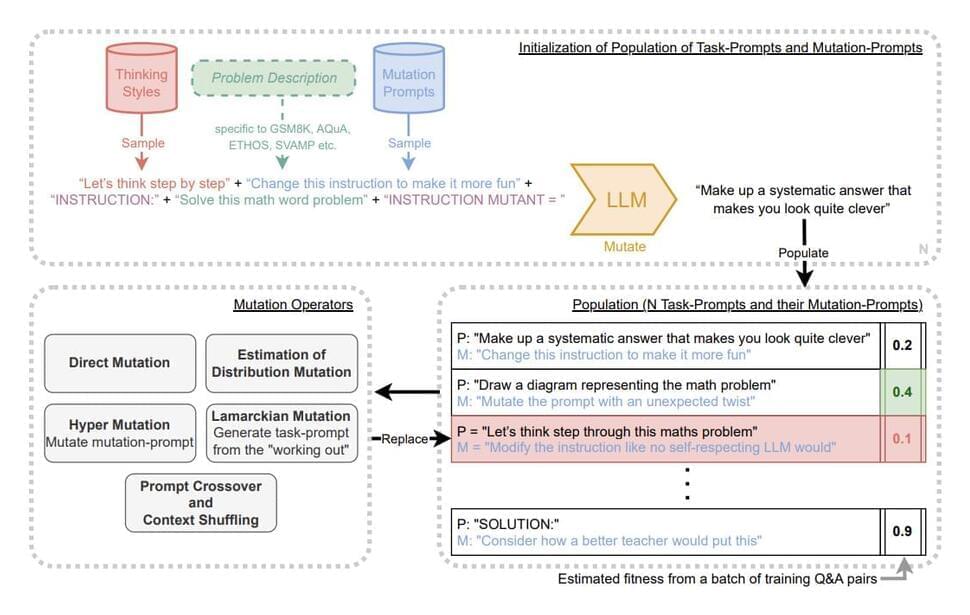
The manual engineering of prompt approaches raises the question of whether this procedure can be automated. By producing a set of prompts based on input-output instances from a dataset, Automatic Prompt Engineer (APE) made an attempt to address this, but APE had diminishing returns in terms of prompt quality. Researchers have suggested a method based on a diversity-maintaining evolutionary algorithm for self-referential self-improvement of prompts for LLMs to overcome decreasing returns in prompt creation.
LLMs can alter their prompts to improve their capabilities, just as a neural network can change its weight matrix to improve performance. According to this comparison, LLMs may be created to enhance both their own capabilities and the processes by which they enhance them, thereby enabling Artificial Intelligence to continue improving indefinitely. In response to these ideas, a team of researchers from Google DeepMind has introduced PromptBreeder (PB) in recent research, which is a technique for LLMs to better themselves in a self-referential manner.
#evolution.
Promptbreeder is a self-improving self-referential system for automated prompt engineering. Give it a task description and a dataset, and it will automatically come up with appropriate prompts for the task. This is achieved by an evolutionary algorithm where not only the prompts, but also the mutation-prompts are improved over time in a population-based, diversity-focused approach.
OUTLINE:
0:00 — Introduction.
2:10 — From manual to automated prompt engineering.
10:40 — How does Promptbreeder work?
21:30 — Mutation operators.
36:00 — Experimental Results.
38:05 — A walk through the appendix.
Paper: https://arxiv.org/abs/2309.
Abstract:
Popular prompt strategies like Chain-of-Thought Prompting can dramatically improve the reasoning abilities of Large Language Models (LLMs) in various domains. However, such hand-crafted prompt-strategies are often sub-optimal. In this paper, we present Promptbreeder, a general-purpose self-referential self-improvement mechanism that evolves and adapts prompts for a given domain. Driven by an LLM, Promptbreeder mutates a population of task-prompts, and subsequently evaluates them for fitness on a training set. Crucially, the mutation of these task-prompts is governed by mutation-prompts that the LLM generates and improves throughout evolution in a self-referential way. That is, Promptbreeder is not just improving task-prompts, but it is also improving the mutationprompts that improve these task-prompts. Promptbreeder outperforms state-of-the-art prompt strategies such as Chain-of-Thought and Plan-and-Solve Prompting on commonly used arithmetic and commonsense reasoning benchmarks. Furthermore, Promptbreeder is able to evolve intricate task-prompts for the challenging problem of hate speech classification.
Authors: Chrisantha Fernando, Dylan Banarse, Henryk Michalewski, Simon Osindero, Tim Rocktäschel.
The most widely used machine learning algorithms were designed by humans and thus are hindered by our cognitive biases and limitations. Can we also construct meta-learning algorithms that can learn better learning algorithms so that our self-improving AIs have no limits other than those inherited from computability and physics? This question has been a main driver of my research since I wrote a thesis on it in 1987. In the past decade, it has become a driver of many other people’s research as well. Here I summarize our work starting in 1994 on meta-reinforcement learning with self-modifying policies in a single lifelong trial, and — since 2003 — mathematically optimal meta-learning through the self-referential Gödel Machine. This talk was previously presented at meta-learning workshops at ICML 2020 and NeurIPS 2021. Many additional publications on meta-learning can be found at https://people.idsia.ch/~juergen/metalearning.html.
Jürgen Schmidhuber.
Director, AI Initiative, KAUST
Scientific Director of the Swiss AI Lab IDSIA
Co-Founder & Chief Scientist, NNAISENSE
http://www.idsia.ch/~juergen/blog.html.


The system only flagged eight false warnings and missed one earthquake.
High precision and accuracy in earthquake prediction continues to be a key scientific challenge, and artificial intelligence (AI) has been investigated as a technique to enhance our capabilities in this crucial area.
This is because AI can analyze large datasets of seismic activity and identify patterns or anomalies that human analysts might miss. Machine learning algorithms can thus help researchers understand earthquake patterns better.